import numpy as np
from matplotlib import pyplot as plt
from matplotlib import patches
import librosa, librosa.display
import pandas as pd
import scipy
from scipy import ndimage
import time
from utils.plot_tools import *
from utils.structure_tools import compute_sm_ti, threshold_matrix, colormap_penalty
from utils.cbar_tools import compute_cens_from_chromagram
import IPython.display as ipd
from IPython.display import Image, Audio
path_img = '../img/8.content-based_audio_retrieval/'
path_data = '../data_FMP/'8.4. 버전 식별
Version Identification
내용 기반 오디오 검색 중 커버 곡이나 리믹스 등 같은 음악의 다른 버전을 인식하는 버전 식별(version identification)에 대해 설명한다. 공통 하위시퀀스 매칭, 매칭의 평가 지표 등에 대해 다룬다.
이 글은 FMP(Fundamentals of Music Processing) Notebooks을 참고로 합니다.
공통 하위시퀀스 매칭 (Common Subsequence Matching)
정렬 시나리오
우선 다양한 정렬(alignment) 시나리오와 그 이면의 원칙에 대해 간략하게 살펴보자. 시퀀스 정렬의 일반적인 목적은 주어진 두 시퀀스 \(X=(x_1,x_2,\ldots,x_N)\) 및 \(Y=(y_1,y_2,\ldots,y_M)\)이 공유하는 유사성 영역을 식별하는 것이다. 동시에, 일치하는 영역의 요소가 대응된다.
일반적으로 정렬의 두 범주인 전역(global) 정렬과 로컬(local) 정렬을 구분할 수 있다. 전역의 경우, 정렬이 두 시퀀스의 전체 길이에 걸쳐 있도록 강제한다. 대조적으로 로컬의 경우에 일반적으로 광범위하게 발산하는 더 긴 시퀀스 내에서 유사성 영역을 식별하려고 시도한다.
동적 시간 워핑(DTW)을 다룰 때 워핑 경로의 개념에 의해 수학적으로 모델링된 전역적 정렬 기술을 접한 적이 있다. 이 정의의 경계 조건(boundary condition)은 두 개의 지정된 시퀀스 \(X\) 및 \(Y\)가 전역적으로 정렬되도록 했다. 또한 단계 크기 조건(step size condition)을 적절하게 수정하여 정렬의 연속성 정도를 조정할 수 있었다.
오디오 매칭에 사용되는 하위 시퀀스(subsequence) DTW에서 두 시퀀스 \(X\) 및 \(Y\)는 다른 방법을 사용해 다뤄졌다. 시퀀스 \(X\)는 전체적으로 정렬되어야 했지만 시퀀스 \(Y\)의 하위 시퀀스만 일치하는 대응 항목으로 충분했다. 따라서 이 시나리오에는 혼합된 전역-로컬 정렬 접근 방식이 필요했다. 기술적으로 시퀀스 \(Y\)에 대한 경계 조건을 완화하여 비용 없이 정렬에서 접미사(suffix)와 접두사(prefix)를 생략할 수 있도록 하는 것이었다.
이 포스트에서는 \(X\) 및 \(Y\) 두 시퀀스 모두에 대해 매칭 하위 시퀀스만 식별되는 로컬 정렬 문제를 처리한다. 매칭을 계산하기 위해 시퀀스 \(X\) 및 \(Y\) 모두에 대한 경계 조건이 제거된다. 또한 두 번째 기술적 수정이 필요하다. 앞의 두 시나리오에서는 적어도 시퀀스 \(X\)의 측면에 전역적 제약이 있는 경우 비용 최소화 경로를 고려하여 정렬을 계산했다. 이제 전역 제약 조건이 없는 로컬 시나리오에서 이러한 접근 방식은 빈 정렬로 이어진다. 따라서 양수 점수(관련 정보) 및 음수 점수(관련 없는 정보)가 있는 점수 매트릭스를 기반으로 점수 최대화 정렬을 살펴봄으로써 다른 최적화 기준을 도입한다.
고려된 경계 조건 외에도 정렬 결과의 특성에 결정적으로 영향을 미치는 다른 요소가 있다. 예를 들어 부분 매칭(partial matching)에서는 단계 크기 조건을 제거하고 훨씬 더 약한 단조성 조건으로 대체한다.
다음 그림은 서로 다른 정렬 시나리오 간의 개념적 차이점을 요약한 것이다.
Image(path_img+"FMP_C7_F23.png" ,width=500)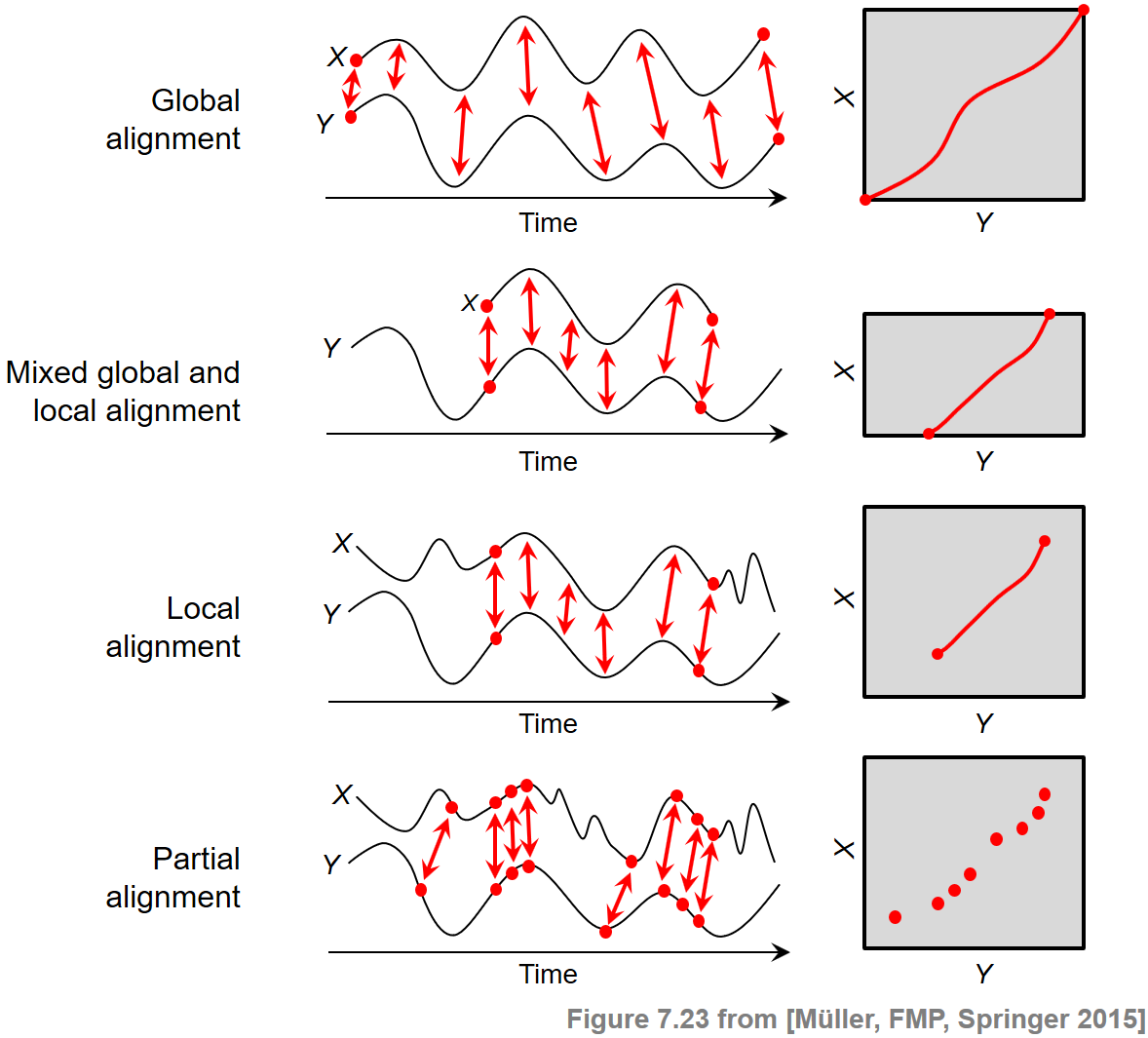
공통 하위시퀀스 매칭 문제의 공식화
버전 식별(version identification)을 위해 로컬 정렬 문제가 필요하며, 이 때 쿼리와 데이터베이스 문서가 특정 부분에서 유사한 톤 진행을 공유한다고 가정하지만 일치가 발생하는 유사성 정도와 기간 또는 위치는 알지 못한다.
이 맥락에서 매칭 작업은 다음과 같이 공식화될 수 있다. 특징 공간에 대해 시퀀스 \(X=(x_1,x_2,\ldots,x_N)\) 및 \(Y=(y_1,y_2,\ldots,y_M)\)가 주어지면 피처 공간 \(\mathcal{F}\)에서 \(X\) 내의 하위 시퀀스와 \(Y\) 내의 하위 시퀀스가 가능한 한 유사하도록 두 하위 시퀀스를 찾는다. 또한 이 두 하위시퀀스의 비교에서 시간적 변형을 처리할 수 있어야 한다.
하위시퀀스 DTW의 경우와 마찬가지로 이 작업은 최적화 문제의 형태로 표현할 수 있으며 동적 프로그래밍을 사용하여 효율적으로 해결할 수 있다. 그러나 주어진 문제에 대해 다른 관점을 가정할 필요가 있다. 하위 시퀀스 DTW에서는 쿼리 \(X\)와 일치하는 \(Y\)의 비용 최소화 하위 시퀀스를 찾았다. 이 최적화 기준은 전체 쿼리 시퀀스 \(X\)가 \(Y\)의 하위 시퀀스와 일치하도록 강제되었기 때문에 작동했다.
이제 \(X\)의 하위 시퀀스만 \(Y\) 중 하나와 일치해야 한다고 가정하면, 빈 하위 시퀀스라는 간단한 방법이 있다. 실제로 두 개의 빈 시퀀스를 일치시키면 전체 비용이 0이 된다. 이는 비용 행렬 \(\mathbf{C}\)에 음수 값이 없다고 가정할 때 최적의 솔루션이다. 하지만 이는 원하는 바가 아니다. 직관적으로 말하면, 최소한의 비용으로 일치시킬 수 있는 하위 시퀀스를 찾고 있을 뿐만 아니라 특정 관련성이 있는 긴 하위 시퀀스도 찾고 있다. 즉, 동시에 두 가지 원칙의 균형을 맞춰야 한다.
- 전체적인 매칭 비용을 최소화하고,
- 하위 시퀀스의 길이를 최대화한다.
이 문제를 해결하기 위해 비용 매트릭스 대신 점수(score) 행렬(또는 유사성(similarity) 행렬)을 사용하여 양의(positive) 관점을 가정한다. 그런 다음 비용을 최소화하는 하위시퀀스를 식별하는 대신 점수를 최대화하는 하위 시퀀스를 찾는다. 하위 시퀀스의 비교에 대한 추가 제약은 적절한 단계 크기(step size) 조건뿐만 아니라 음의 페널티 값을 도입하여 부과한다.
유사성 측정 \(s:\mathcal{F}\times\mathcal{F}\to \mathbb{R}\)를 고정하면 다음을 설정하여 \(N\times M\) 점수 행렬을 계산할 수 있다. \[\mathbf{S}(n,m):=s(x_n,y_m)\] for \(n\in[1:N]\) and \(m\in[1:M]\)
이 점수 행렬의 속성은 자기 유사성 행렬의 경우에 대해서 설명했던 것과 동일한 향상을 사용하여 더욱 향상될 수 있다. 특히 임계값 파라미터 \(\tau>0\)와 페널티 파라미터 \(\delta\leq 0\)에 대한 임계값 적용은 중요한 단계이다.
관련 유사성 관계를 나타낼 수 있는 셀은 양의 점수를 갖는 반면 다른 모든 셀에는 음의 점수를 부여하는 방식으로 점수 행렬이 구성된다. 이 속성은 가능한 큰 점수를 누적하는 경로 구성 요소를 찾으려고 시도하는 다음의 절차에서 중요하다. 이러한 경로는 주로 \(\mathbf{S}\)의 양수 부분에 있으며 음수 점수의 셀을 통과하는 것을 피한다.
공통 하위 시퀀스를 찾는 문제를 더 공식화하려면 두 피쳐 시퀀스를 비교할 때 시간적 변형을 설명하는 경로 개념이 필요하다. 자기 유사성 행렬의 맥락에서와 같이 경로는 시퀀스 \(P=((n_1,m_1), \ldots,(n_L,m_L))\)로 정의된다. 이 때 셀 \((n_\ell,m_\ell)\in[1:N]\times[1:M]\), $ $이며, 허용되는 단계 크기의 집합 \(\Sigma\)에 대해 \((n_{\ell+1},m_{\ell+1}) -(n_\ell,m_\ell)\in \Sigma\)를 만족한다.
따라서 \(\Sigma=\{(0,1),(1,0),(1,1)\}\)를 선택하면 이 정의는 경계 조건을 생략한 것 빼고는 워핑 경로에 대한 정의와 동일하다. 그 이유는 시퀀스 \(X\) 및 \(Y\)를 전체적으로 정렬하지 않고 하위 시퀀스만 정렬하기 때문이다. 경로 \(P\)에 대해 유도된(induced) 세그먼트 \(\pi_1(P):=[n_1:n_L]\) 및 \(\pi_2(P):=[m_1:m_L]\)를 연결한다. \(P\)의 점수 \(\sigma(P)\)는 \(\sigma(P) := \sum_{\ell=1}^L s(n_\ell,m_\ell)\)로 정의된다.
이러한 정의를 사용하여 가능한 모든 경로(임의의 시작 및 끝 위치 포함)에서 점수 최대화 경로 \(P^\ast := \underset{P}{\mathrm{argmax}} \,\,\sigma(P)\)를 찾는 최적화 작업을 진행한다. \(X\) 및 \(Y\)의 가장 잘 일치하는 두개의 하위 시퀀스는 유도된 세그먼트 \(\pi_1(P^\ast)\) 및 \(\pi_2(P^\ast)\)에 의해 각각 주어진다.
동적 프로그래밍을 사용한 최적화 알고리즘
점수 극대화 경로는 DTW 알고리즘과 비슷하게 동적 프로그램(DP)로 계산될 수 있다. 이를 위해 \(N\times M\) 누적 점수 행렬 (accumulated score matrix) \(\mathbf{D}\)를 다음과 같이 정의한다. \[\mathbf{D}(n,m) := \max\{\sigma(P) \mid \mbox{$P$ is path ending at $(n,m)$ }\}\] for \(n\in[1:N]\) and \(m\in[1:M]\).
다시 말해, \(\mathbf{D}(n,m)\)는 임의의 셀에서 시작하여 \((n,m)\)에서 끝나는 경로로 누적된 가능한 최대 점수이다. 이 정의에 따르면, 빈 경로 \(P=\emptyset\)는 점수 \(\sigma(P)=0\)의 경로로 생각될 수 있다. \(n=1\) 혹은 \(m=1\)의 셀 \((n,m)\)에 대해 다음을 얻을 수 있다. \[\mathbf{D}(1,1)=\max\big\{0,\mathbf{S}(1,1)\big\}\] \[\mathbf{D}(n,1)=\max\big\{0,\mathbf{D}(n-1,1)+\mathbf{S}(n,1)\big\} \mbox{ for } n\in [2:N]\] \[\mathbf{D}(1,m)=\max\big\{0,\mathbf{D}(1,m-1)+\mathbf{S}(1,m)\big\} \mbox{ for } m\in [2:M]\]
- 이는 재귀(recursion)에 대한 바운더리를 구성한다
\(n\in [2:N]\)와 \(m\in [2:M]\)에 대해서는 다음을 통해 \(\mathbf{D}\)를 계산할 수 있다. \[\mathbf{D}(n,m)= \max\left\{ \begin{array}{l} 0, \\ \mathbf{D}(n-1,m-1) + \mathbf{S}(n,m), \\ \mathbf{D}(n-1,m) + \mathbf{S}(n,m), \\ \mathbf{D}(n,m-1)+ \mathbf{S}(n,m) \end{array}\right.\]
이 재귀는 두 가지 면에서 DTW에 사용되는 것과 다르다.
- 첫째, 초과 비용을 최소화하는 대신 초과(음수일 수 있음) 점수를 최대화한다.
- 두 번째 차이점은 최대화에 0값이 포함된다는 것이다. 이를 통해 잠재적으로 음의 점수를 누적하지 않고도 모든 위치에서 경로를 시작할 수 있다. 이는 시퀀스 \(X\)와 \(Y\)를 비교할 때 시작 부분을 건너뛸 수 있다는 아이디어를 실현한다.
고려된 경로에 경계 제약을 두지 않기 때문에, 점수 최대화 경로 \(P^\ast\)는 임의의 셀에서 끝날 수 있다. 따라서 가능한 모든 경로에서 최대 점수를 얻으려면 \(\mathbf{D}\)의 최대 항목을 살펴봐야 한다. \[\mathbf{D}^\mathrm{max}:=\sigma(P^\ast)=\max_{(n,m)\in[1:N]\times[1:M]}\mathbf{ D}(n,m).\]
일반적으로 최대값을 갖는 \(\mathbf{D}\) 항목이 여러 개 있을 수 있다. 최적 경로 \(P^\ast\)의 끝 위치를 정의하는 \(q_1\)와 같은 항목 중 하나로 시작한다. 전체 경로는 DTW에서와 마찬가지로 역추적(backtracking)을 통해 얻는다.
그러나 이번에는 역추적의 정지 조건(stop condition)이 다르다. \(q_1,q_2,\ldots,q_\ell\)을 반복적으로 결정된 셀이라고 하면, 역추적은 셀 \(q_\ell=(a,b)\)이 \(\mathbf{D}(a ,b)=0\) 또는 \(q_\ell=(1,1)\)에 도달하면 멈춘다.
첫 번째 경우 \(q_\ell=(a,b)\) 셀은 비양수(nonpositive) 점수 \(\mathbf{S}(a,b)\leq 0\)이므로 제외된다. 이렇게 하면 최적의 경로 \(P^\ast=(q_{\ell-1},\ldots,q_1)\)가 생성된다. 두 번째 경우 경로는 \(\mathbf{S}(1,1)>0\)인 경우 \(q_\ell=(1,1)\) 셀로 시작하거나, \(\mathbf{S}(1,1)\leq 0\)인 경우 셀 \(q_{\ell-1}\)로 시작한다.
간단한 예
- 이 절차를 설명하기 위해 두 시퀀스 \(X=(x_1,\ldots,x_5)\) 및 \(Y=(y_1,\ldots,y_6)\)에 대한 예를 보자. 시퀀스와 로컬 유사성 측정을 명시적으로 지정하는 대신 이 예에서 유사성 행렬 \(\mathbf{S}\)가 직접 주어진다고 가정한다. 다음 그림은 \(\mathbf{S}\) 및 결과 누적 점수 행렬 \(\mathbf{D}\)를 보여준다. \(\mathbf{D}\) 행렬은 \((3,5)\) 셀에서 최대값을 가정한다. 역추적은 점수 최대화 경로 \(P^\ast = ((1,3),(2,3),(2,4),(3,5))\), \(\sigma(P^\ast)= 5\)를 얻는다. 유도된 두 개의 세그먼트는 \(\pi_1(P^\ast)=[1:3]\) 및 \(\pi_2(P^\ast)=[3:5]\)이며, 이는 하위 시퀀스 \((x_1,x_2,x_3 )\) 및 \((y_3,y_4,y_5)\)를 얻는다.
Image(path_img+"FMP_C7_F20.png", width=600)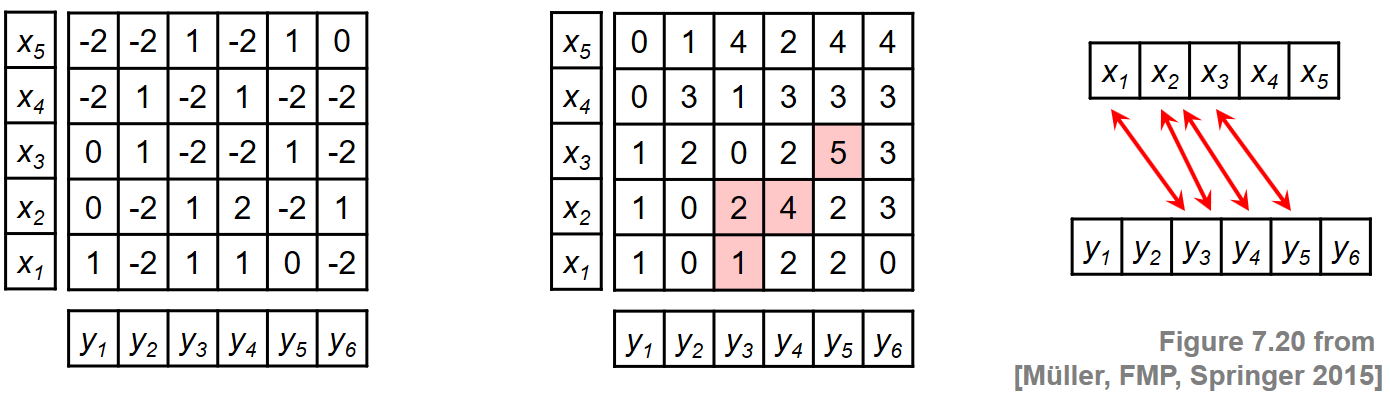
# Example from Figure 7.20, [Müller, FMP, Springer 2015]
S = np.array([[1, -2, 1, 1, 0, -2],
[0, -2, 1, 2, -2, 1],
[0, 1, -2, -2, 1, -2],
[-2, 1, -2, 1, -2, -2],
[-2, -2, 1, -2, 1, 0]])
print('Score matrix S = ', S, sep='\n')Score matrix S =
[[ 1 -2 1 1 0 -2]
[ 0 -2 1 2 -2 1]
[ 0 1 -2 -2 1 -2]
[-2 1 -2 1 -2 -2]
[-2 -2 1 -2 1 0]]def compute_accumulated_score_matrix_common_subsequence(S):
"""Given the score matrix, compute the accumulated score matrix
for common subsequence matching with step sizes {(1, 0), (0, 1), (1, 1)}
Args:
S (np.ndarray): Score matrix
Returns:
D (np.ndarray): Accumulated score matrix
"""
N, M = S.shape
D = np.zeros((N, M))
D[0, 0] = max(0, S[0, 0])
for n in range(1, N):
D[n, 0] = max(0, D[n-1, 0] + S[n, 0])
for m in range(1, M):
D[0, m] = max(0, D[0, m-1] + S[0, m])
for n in range(1, N):
for m in range(1, M):
D[n, m] = max(0, D[n-1, m-1] + S[n, m], D[n-1, m] + S[n, m], D[n, m-1] + S[n, m])
return DD = compute_accumulated_score_matrix_common_subsequence(S)
Dmax = np.max(D)
n, m = divmod(np.argmax(D), D.shape[1])
print('Accumulated score matrix D = ', D, sep='\n')
print('Maximal accumulated score Dmax = ', Dmax)
print('Maximizing cell (n,m) = (%d,%d)' % (n, m))Accumulated score matrix D =
[[1. 0. 1. 2. 2. 0.]
[1. 0. 2. 4. 2. 3.]
[1. 2. 0. 2. 5. 3.]
[0. 3. 1. 3. 3. 3.]
[0. 1. 4. 2. 4. 4.]]
Maximal accumulated score Dmax = 5.0
Maximizing cell (n,m) = (2,4)- 마지막으로 역추적을 사용하여 최적 경로 \(P^\ast\)와 유도된 세그먼트 \(\pi_1(P^\ast)\)와 \(\pi_2(P^\ast)\)를 얻는다.
def compute_optimal_path_common_subsequence(D, cellmax=True, n=0, m=0):
"""Given an accumulated score matrix, compute the score-maximizing path
for common subsequence matching with step sizes {(1, 0), (0, 1), (1, 1)}
Args:
D (np.ndarray): Accumulated score matrix
cellmax (bool): If "True", score-maximizing cell will be computed (Default value = True)
n (int): Index (first axis) of cell for backtracking start; only used when cellmax=False (Default value = 0)
m (int): Index (second axis) of cell for backtracking start; only used when cellmax=False (Default value = 0)
Returns:
P (np.ndarray): Score-maximizing path (array of index pairs)
"""
if cellmax:
# n, m = np.unravel_index(np.argmax(D), D.shape) # doesn't work with jit
n, m = divmod(np.argmax(D), D.shape[1])
P = [(n, m)]
while ((n, m) != (0, 0) and (D[n, m] != 0)):
if n == 0:
cell = (0, m-1)
elif m == 0:
cell = (n-1, 0)
else:
val = max(D[n-1, m-1], D[n-1, m], D[n, m-1])
if val == D[n-1, m-1]:
cell = (n-1, m-1)
elif val == D[n-1, m]:
cell = (n-1, m)
else:
cell = (n, m-1)
P.append(cell)
n, m = cell
if (D[n, m] == 0):
del P[-1]
P.reverse()
P = np.array(P)
return P
def get_induced_segments(P):
"""Given a path, compute the induces segments
Args:
P (np.ndarray): Path (list of index pairs)
Returns:
seg_X (np.ndarray): Induced segment of first sequence
seg_Y (np.ndarray): Induced segment of second sequence
"""
seg_X = np.arange(P[0, 0], P[-1, 0] + 1)
seg_Y = np.arange(P[0, 1], P[-1, 1] + 1)
return seg_X, seg_Y
P = compute_optimal_path_common_subsequence(D)
seg_X, seg_Y = get_induced_segments(P)
print('Optimal path P =', P, sep='\n')
print('Induced segment for X:', seg_X)
print('Induced segment for Y:', seg_Y)Optimal path P =
[[0 2]
[0 3]
[1 3]
[2 4]]
Induced segment for X: [0 1 2]
Induced segment for Y: [2 3 4]# a sanity check
score_P = sum(S[n, m] for (n, m) in P)
print('Total score of optimal path:', score_P)
print('Maximal accumulated score Dmax = ', Dmax)Total score of optimal path: 5
Maximal accumulated score Dmax = 5.0plt.figure(figsize=(9, 3))
plt.subplot(1, 2, 1)
plt.imshow(S, cmap='PuOr', origin='lower', aspect='equal')
plt.plot(P[:, 1], P[:, 0], marker='o', color='r')
plt.clim([np.min(S), np.max(S)])
plt.colorbar()
plt.title('$\mathbf{S}$ with optimal path')
plt.xlabel('Sequence Y')
plt.ylabel('Sequence X')
plt.subplot(1, 2, 2)
plt.imshow(D, cmap='gray_r', origin='lower', aspect='equal')
plt.plot(P[:, 1], P[:, 0], marker='o', color='r')
plt.clim([0, np.max(D)])
plt.colorbar()
plt.title('$\mathbf{D}$ with optimal path')
plt.xlabel('Sequence Y')
plt.ylabel('Sequence X')
plt.tight_layout()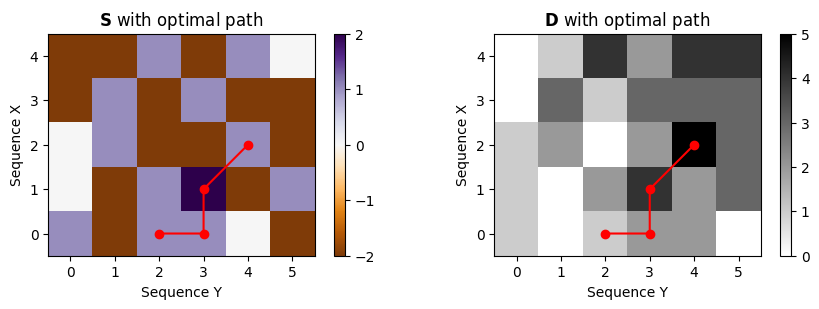
부분 매칭 (Partial Matching)
단계 크기(step size) 조건을 훨씬 더 약한 단조성(monotonicity) 조건으로 대체하여 정렬 요구 사항을 더 완화할 수 있다. 이에 대해 부분 매칭(parital matching)이라는 최적화 문제를 생각할 수 있다.
이 문제를 공식화하고 동적 프로그래밍을 기반으로 효율적인 알고리즘을 보도록 한다. \(X=(x_1,x_2,\ldots,x_N)\) 및 \(Y=(y_1,y_2,\ldots,y_M)\)가 특징 공간 \(\mathcal{F}\)에 대한 두 시퀀스라고 가정한다. \(X\)와 \(Y\) 사이의 길이 \(L\in\mathbb{N}_0\)의 부분 매칭은 셀 \((n_\ell,m_\ell)\in[1:N]\times[1:M]\), \(\ell\in[1:L]\)의 시퀀스 \(P=((n_1,m_1), \ldots,(n_L, m_L))\)로 정의되며, 강하게 단조 증가한다: \[n_1<n_2<\ldots < n_L \quad\mbox{and}\quad m_1< m_2< \ldots < m_L\]
유사성 척도 \(s:\mathcal{F}\times\mathcal{F}\to \mathbb{R}\)가 주어지면 유사성 행렬 \(\mathbf{S}\)를 \(\mathbf{S}(n ,m):=s(x_{n},y_{m})\)로 정의한다. 그런 다음 부분 매칭 \(P\)의 총 점수 \(\sigma(P)\)는 \(\sigma(P) := \sum_{\ell = 1}^{L} \mathbf{S}(n_\ell,m_\ell)\)로 구체화된다.
Image(path_img+"FMP_C7_E10.png", width=600)
“nested” 루프에서 점수 값 \(\mathbf{S}(n,m)\)는 DTW 알고리즘과 달리 대각선 스텝 크기의 경우에만 추가된다. 여기서 비용 값 \(\mathbf{C}(n,m)\)는 세 스텝 크기 모두의 경우에 추가된다. 또한 누적 점수 \(\mathbf{D}(n,m)\)를 산출하는 최적의 부분 매칭은 \(\mathbf{D}(n,m)\)를 산출하는 최적의 워핑 경로가 항상 \((n,m)\) 셀로 끝나는 DTW 알고리즘과 달리 반드시 셀 \((n,m)\)에서 끝나지는 않는다.
다음 코드 셀에서는 부분 매칭 절차에 대한 참조 구현을 제공한다.
def compute_partial_matching(S):
"""Given the score matrix, compute the accumulated score matrix
for partial matching
Args:
S (np.ndarray): Score matrix
Returns:
D (np.ndarray): Accumulated score matrix
P (np.ndarray): Partial match (array of index pairs)
"""
N, M = S.shape
D = np.zeros((N+1, M+1))
for n in range(1, N+1):
for m in range(1, M+1):
D[n, m] = max(D[n, m-1], D[n-1, m], D[n-1, m-1] + S[n-1, m-1])
P = []
n = N
m = M
while (n > 0) and (m > 0):
if D[n, m] == D[n, m-1]:
m = m - 1
elif D[n, m] == D[n-1, m]:
n = n - 1
else:
P.append((n-1, m-1))
n = n - 1
m = m - 1
P.reverse()
P = np.array(P)
return D, PD, P = compute_partial_matching(S)
plt.figure(figsize=(9, 3))
plt.subplot(1, 2, 1)
plt.imshow(S, cmap='PuOr', origin='lower', aspect='equal')
plt.plot(P[:, 1], P[:, 0], marker='o', color='r', linestyle='')
plt.clim([np.min(S), np.max(S)])
plt.colorbar()
plt.title('$\mathbf{S}$ with optimal match')
plt.xlabel('Sequence Y')
plt.ylabel('Sequence X')
plt.subplot(1, 2, 2)
plt.imshow(D, cmap='gray_r', origin='lower', aspect='equal')
plt.plot(P[:, 1]+1, P[:, 0]+1, marker='o', color='r', linestyle='')
plt.clim([0, np.max(D)])
plt.colorbar()
plt.title('$\mathbf{D}$ with optimal match')
plt.xlabel('Sequence Y')
plt.ylabel('Sequence X')
plt.tight_layout()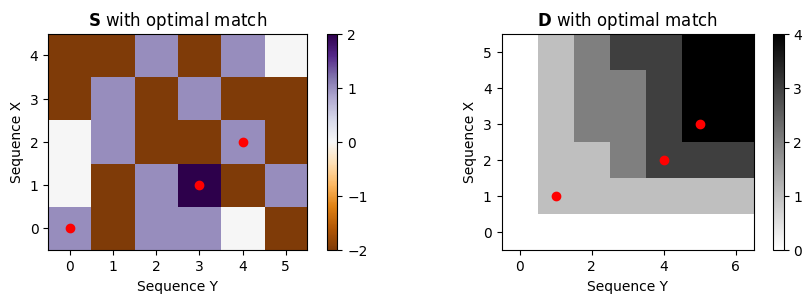
버전 식별 (Version Identification)
버전 식별(version identification)이라는 작업은 커버 송 검색(cover song retrieval)이라고도 불린다. 음악 작품의 녹음(또는 그 일부)이 주어지면 버전 식별은 음악 컬렉션에서 동일한 작품의 모든 녹음 버전(예: 커버 곡)을 자동으로 검색하는 것을 목표로 한다.
- 버전 식별에서 쿼리는 일반적으로 작은 오디오 조각의 쿼리를 기반으로 하는 오디오 식별 및 오디오 매칭과 달리 전체 녹음으로 구성되다.
- 따라서 버전 식별은 일반적으로 전체 문서를 전체적으로 비교하기 위해 단일 유사성 측정이 사용되는 문서 수준(document-level) 검색 작업으로 간주된다.
- 버전 식별의 기본 가정은 음악 작품의 원본 버전과 파생 버전이 일반적으로 몇 가지 공통된 특성을 공유한다는 것이다. 그러나 버전 간의 가능한 구조적(structural) 차이로 인해 이러한 공통 요소가 발생하는 위치가 명확하지 않다.
- 주어진 쿼리 문서와 데이터베이스 문서 간의 전역(global) 유사성을 평가할 때 버전 식별의 일반적인 전략은 특정 음악적 속성과 관련하여 로컬(local) 동시성을 찾는 것이다. 즉, 전역 비교는 로컬 기준으로 수행된다.
새 버전을 만들 때 적용될 수 있는 많은 종류의 수정을 고려할 때, 단일 기술을 사용하여 모든 변형을 처리할 수 있다고 가정하는 것은 현실적이지 않다.
다음에서는 식별할 버전이 적어도 특정 섹션에서 유사한 선율 또는 화성 진행을 공유하는 경우로 제한한다. 반면에 템포, 악기 편성, 음색, 전체적인 음악적 구조와 같은 측면에서의 차이는 허용한다.
임의 길이의 두 개의 오디오 녹음(문서라고도 함)이 주어지면 단계는 다음과 같다.
- 먼저 음조(tonal) 특성을 캡처하기 위해 녹음을 크로마 기반 오디오 특징의 시퀀스로 변환한다.
- 둘째, 점수 행렬(또는 유사성 행렬)은 이 두 시퀀스의 요소를 쌍(pairs)으로 비교하여 계산된다.
- 셋째, 잠재적으로 긴 높은 유사성의 경로를 식별한다. 이러한 경로의 존재는 두 크로마 시퀀스가 일부 관련 하위 시퀀스를 공유함을 나타낸다.
- 마지막으로 이 정보에서 비교할 두 버전 간의 유사성 점수를 도출한다.
Image(path_img+"FMP_C7_F18.png", width=600)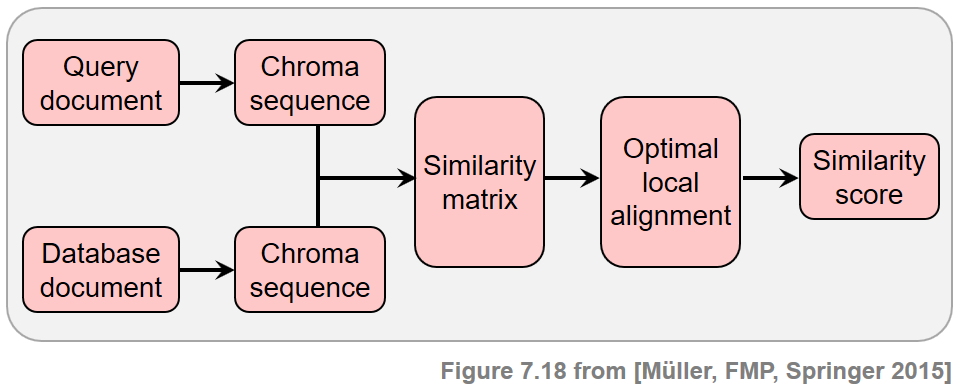
점수 행렬의 계산
첫 번째 단계에서 쿼리와 데이터베이스 문서는 \(X=(x_1,x_2,\ldots,x_N)\) 및 \(Y=(y_1,y_2,\ldots,y_M)\)과 같이 크로마 기반 특징 시퀀스로 변환된다. 뉘앙스를 혼합하고 싶기 때문에 CENS 특징과 같이 매끄럽고 정규화된 크로마 변형을 사용하는 것이 좋다.
버전 식별에서 오디오 매칭과 유사하게 \(2~\mathrm{Hz}\)(초당 두 개의 크로마 벡터)의 피쳐 레이트(feature rate)는 견고성과 특이성 간의 좋은 트레이드 오프 관계를 구성한다.
시퀀스 \(X\) 및 \(Y\)가 주어졌을 때, 최대한 유사한 \(X\) 내의 하위 시퀀스와 \(Y\) 내의 하위 시퀀스를 찾는다. 이를 위해 로컬 정렬을 계산한다. 이 점수 최대화 정렬 기법을 사용하려면 양인 점수를 가진 셀은 \(X\)와 \(Y\) 사이의 잠재적 관계를, 음의 점수를 가진 셀은 관련 없는 정보를 인코딩하는 점수 행렬을 입력해야 한다.
이러한 점수 행렬을 구성하기 위해 자기유사성 행렬(SSM)을 구성하는 과정에서 보았던 것과 유사한 기술을 적용한다.
- 시퀀스 \(X\) 및 \(Y\)의 요소를 쌍으로 비교하여 첫 번째 점수 행렬을 얻는다. 정규화된 CENS 벡터에 적용된 내적을 로컬 유사성 측정으로 사용한다. 이 행렬에서 유사도가 높은 경로는 유사한 하위 시퀀스를 나타낸다.
- 정보를 향상시키기 위해 경로 향상 전략을 적용한다.
- 다른 음악 키를 설명하기 위해 조옮김 불변 SSM에서 사용된 아이디어를 적용할 수 있다.
- 양수 값과 음수 값 사이의 균형을 얻기 위해 정규화 및 페널티와 함께 임계값 절차를 적용한다. 특히 가장 높은 값을 가진 셀의 \(15\) 퍼센트를 유지하는 임계값(
thresh=0.15)을 위해 상대 전략(strategy = relative)을 사용한다. 또한 0과 1 사이의 양수 범위를 재조정한다(scale=1). 다른 모든 셀은 관련이 없는 것으로 간주되며 음수 점수 값(penalty=-2)으로 설정된다.
다음 코드 셀에서 “Day Tripper”라는 노래에 대해 표시되는 점수 행렬을 계산한다. 세로축은 원래 Beatles 버전에 해당하고 가로축은 Ocean Color Scene의 커버 버전에 해당한다.
def compute_sm_from_wav(x1, x2, Fs, N=4410, H=2205, ell=21, d=5, L_smooth=12,
tempo_rel_set=np.array([0.66, 0.81, 1, 1.22, 1.5]),
shift_set=np.array([0]), strategy='relative', scale=True,
thresh=0.15, penalty=-2.0, binarize=False):
"""Compute a similarity matrix (SM)
Args:
x1 (np.ndarray): First signal
x2 (np.ndarray): Second signal
Fs (scalar): Sampling rate of WAV files
N (int): Window size for computing STFT-based chroma features (Default value = 4410)
H (int): Hop size for computing STFT-based chroma features (Default value = 2205)
ell (int): Smoothing length for computing CENS features (Default value = 21)
d (int): Downsampling factor for computing CENS features (Default value = 5)
L_smooth (int): Length of filter for enhancing SM (Default value = 12)
tempo_rel_set (np.ndarray): Set of relative tempo values for enhancing SM
(Default value = np.array([0.66, 0.81, 1, 1.22, 1.5]))
shift_set (np.ndarray): Set of shift indices for enhancing SM (Default value = np.array([0]))
strategy (str): Thresholding strategy for thresholding SM ('absolute', 'relative', 'local')
(Default value = 'relative')
scale (bool): If scale=True, then scaling of positive values to range [0,1] for thresholding SM
(Default value = True)
thresh (float): Treshold (meaning depends on strategy) (Default value = 0.15)
penalty (float): Set values below treshold to value specified (Default value = -2.0)
binarize (bool): Binarizes final matrix (positive: 1; otherwise: 0) (Default value = False)
Returns:
X (np.ndarray): CENS feature sequence for first signal
Y (np.ndarray): CENS feature sequence for second signal
Fs_feature (scalar): Feature rate
S_thresh (np.ndarray): Similarity matrix
I (np.ndarray): Index matrix
"""
# Computation of CENS features
C1 = librosa.feature.chroma_stft(y=x1, sr=Fs, tuning=0, norm=1, hop_length=H, n_fft=N)
C2 = librosa.feature.chroma_stft(y=x2, sr=Fs, tuning=0, norm=1, hop_length=H, n_fft=N)
Fs_C = Fs / H
X, Fs_feature = compute_cens_from_chromagram(C1, Fs_C, ell=ell, d=d)
Y, Fs_feature = compute_cens_from_chromagram(C2, Fs_C, ell=ell, d=d)
# Compute enhanced SM
S, I = compute_sm_ti(X, Y, L=L_smooth, tempo_rel_set=tempo_rel_set,
shift_set=shift_set, direction=2)
S_thresh = threshold_matrix(S, thresh=thresh, strategy=strategy,
scale=scale, penalty=penalty, binarize=binarize)
return X, Y, Fs_feature, S_thresh, Ifn1 = 'FMP_C7_F19_TheBeatles_DayTripper_TheBeatles.wav'
fn2 = 'FMP_C7_F19_TheBeatles_DayTripper_OceanColourScene.wav'
x1, Fs = librosa.load(path_data+fn1)
x2, Fs = librosa.load(path_data+fn2)
penalty=-2
tempo_rel_set=np.array([0.8, 1, 1.2])
L_smooth = 20
X, Y, Fs_X, S, I = compute_sm_from_wav(x1, x2, Fs, tempo_rel_set = tempo_rel_set,
L_smooth=L_smooth, penalty=penalty)
cmap_penalty = colormap_penalty(penalty=penalty)
figsize=(8, 4)
plot_matrix(S, figsize=figsize, cmap=cmap_penalty,
Fs=Fs_X, Fs_F=Fs_X, aspect='equal',
title='Score matrix $\mathbf{S}$',
xlabel='Time (seconds) [Ocean Colour Scene]',
ylabel='Time (seconds) [Beatles]')
plt.tight_layout()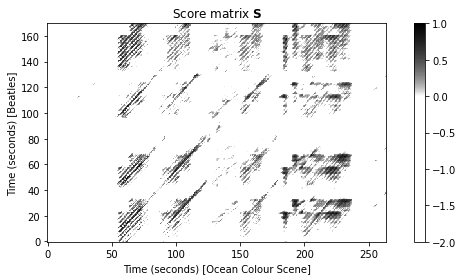
공통 하위시퀀스 매칭
이 점수 매트릭스에서 \(\mathbf{S}\)의 양수 부분에 있는 많은 경로 구성 요소를 명확하게 확인 할 수 있다. 반면 커버 버전의 시작과 끝 부분에는 경로 같은 구조가 없다. 위에서 언급했듯이 처음 50초 동안 밴드 멤버들은 원래 비틀즈 버전과 음색(tonal) 관계가 없도록 청중과 상호 작용하고 대화한다.
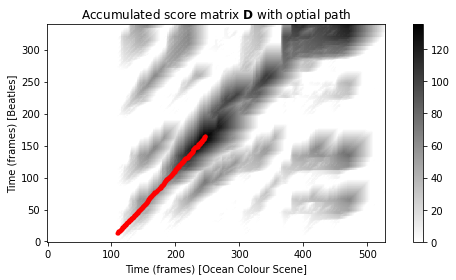
다음 코드 셀에서는 유사성이 높은 잠재적으로 긴 경로를 식별하기 위해 공통 하위시퀀스 매칭(common subsequence matching)를 사용한다. 그림은 점수 행렬 \(\mathrm{S}\)와 누적 점수 행렬 \(\mathrm{D}\)를 각각 최적의 경로와 함께 보여준다.
D = compute_accumulated_score_matrix_common_subsequence(S)
Dmax = np.max(D)
n, m = divmod(np.argmax(D), D.shape[1])
P = compute_optimal_path_common_subsequence(D)
seg_X, seg_Y = get_induced_segments(P)
figsize = (8, 4)
plot_matrix(S, figsize=figsize, cmap=cmap_penalty, Fs=1, Fs_F=1, aspect='equal',
title='Score matrix $\mathbf{S}$ with optimal path',
xlabel='Time (frames) [Ocean Colour Scene]',
ylabel='Time (frames) [Beatles]')
plt.plot(P[:, 1], P[:, 0], marker='.', color='r')
plt.tight_layout()
figsize = (8, 4)
plot_matrix(D, figsize=figsize, cmap='gray_r', Fs=1, Fs_F=1, aspect='equal',
title='Accumulated score matrix $\mathbf{D}$ with optial path',
xlabel='Time (frames) [Ocean Colour Scene]',
ylabel='Time (frames) [Beatles]')
plt.plot(P[:, 1], P[:, 0], marker='.', color='r')
plt.tight_layout()
plt.show()
print('Maximal accumulated score Dmax = %.2f' % Dmax)
print('Maximizing cell (n, m) = (%d, %d)' % (n, m))
print('Induced segment for X: [%d:%d]' % (seg_X[0], seg_X[-1]))
print('Induced segment for Y: [%d:%d]' % (seg_Y[0], seg_Y[-1]))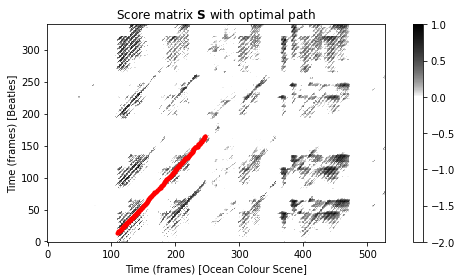
Maximal accumulated score Dmax = 135.52
Maximizing cell (n, m) = (165, 247)
Induced segment for X: [13:165]
Induced segment for Y: [109:247]이전 그림에서 축은 프레임으로 주어진다. \(\mathbf{S}\)에서 가장 긴 연속 경로는 셀 \((13,109)\)에서 시작하여 셀 \((165,247)\)에서 끝나는 대각선 방향이다.
\(\mathbf{D}\)의 최대 항목은 다음과 같다. \[\mathbf{D}^\mathrm{max} = \mathbf{D}(165,247) = 135.52\]
일치하는 공통 하위시퀀스는 \(X[13:165]\)(비틀즈 버전의 경우) 및 \(Y[109:247]\)(커버 버전의 경우)이다. 피쳐 레이트가 \(2~\mathrm{Hz}\)인 것을 고려하면 비틀즈 녹음의 섹션은 대략 \(76~\mathrm{sec}\)의 길이를 갖는 반면, 커버 곡에서 정렬된 섹션의 길이는 \(69~\mathrm{sec}\)이다. 이것은 다시 원래 버전의 템포가 Ocean Color Scene의 커버 버전보다 느리다는 것을 나타낸다.
다음 코드 셀에서 이번에는 초 단위로 지정된 축을 사용하여 최적의 경로와 함께 점수 행렬을 다시 시각화한다. 유도된 세그먼트는 녹색 선으로 표시된다.
figsize = (8, 4)
plot_matrix(S, figsize=figsize, cmap=cmap_penalty, Fs=Fs_X, Fs_F=Fs_X, aspect='equal',
title='Score matrix $\mathbf{S}$ with optimal path',
xlabel='Time (seconds) [Ocean Colour Scene]',
ylabel='Time (seconds) [Beatles]')
plt.plot(P[:, 1] / Fs_X, P[:, 0] / Fs_X, marker='.', color='r')
start_X, start_Y = P[0, :] / Fs_X
end_X, end_Y = P[-1, :] / Fs_X
plt.plot([0, 0], [start_X, end_X], c='g', linewidth=7)
plt.plot([start_Y, end_Y], [0, 0], c='g', linewidth=7)
plt.plot([0, start_Y], [start_X, start_X], c='r', linestyle=':')
plt.plot([0, end_Y], [end_X, end_X], c='r', linestyle=':')
plt.plot([start_Y, start_Y], [0, start_X], c='r', linestyle=':')
plt.plot([end_Y, end_Y], [0, end_X], c='r', linestyle=':')
plt.tight_layout()
plt.show()
print('Induced segment of the original version (Beatles):')
ipd.display(Audio(x1[int(start_X * Fs):int(end_X * Fs)], rate=Fs))
print('Induced segment of the cover version (Ocean Colour Scene):')
ipd.display(Audio(x2[int(start_Y * Fs):int(end_Y * Fs)], rate=Fs))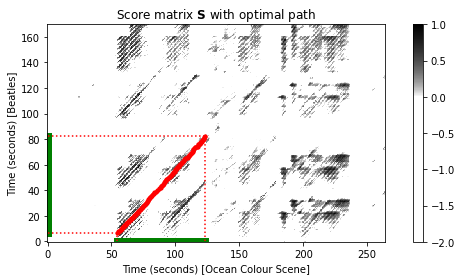
Induced segment of the original version (Beatles):Induced segment of the cover version (Ocean Colour Scene):평가 지표
문서-수준 검색
버전 식별과 같은 문서 수준(document-level) 검색 시나리오에서 목표는 조각이 아닌 전체 문서를 검색하는 것이다(문서 수준 유사성 점수가 공통 하위 시퀀스의 로컬 일치를 기반으로 할 수 있음).
다음에서 데이터베이스는 \(K\)개의 문서, \({\mathcal{D}_1,\mathcal{D}_2,\ldots,\mathcal{D}_K\ }\)의 집합으로 구성되어 있다고 가정한다. 문서 \(\mathcal{D}_k\)는 식별자 \(k\in[1:K]\)와 관련된다.
또한 쿼리 문서 \(\mathcal{Q}\)가 주어지면 각 \(k\in[1:K]\)에 대해 \(\gamma(\mathcal{Q},\mathcal{D}_k)\in\mathbb{R}\) 값을 산출하는 유사성 측도가 있다고 가정한다.
이러한 값을 기반으로 유사성 값의 내림차순으로 데이터베이스 문서를 순위(즉, 정렬)매길 수 있다. 이와 같이 주어진 쿼리와 가장 유사한 검색 결과가 사용자에게 표시되는 결과 목록의 앞부분에 나타난다. 최상위(top rank)는 검색 결과 1위(즉, 유사도가 가장 높은 문서)의 검색 결과이다.
또한 \(k,\ell \in[1:K]\)에 대해 \(\gamma(\mathcal{Q},\mathcal {D}_k)>\gamma(\mathcal{Q},\mathcal{D}_\ell)\)이면 \(\mathcal{D}_k\)가 \(\mathcal{D}_\ell\)보다 높은 순위를 갖는다고 한다.
\(\gamma(\mathcal{Q},\mathcal{D}_k)=\gamma(\mathcal{Q},\mathcal{D}_\ell)\)의 경우, \(\mathcal{D}_k\)는 \(k<\ell\)일 때 \(\mathcal{D}_\ell\)보다 순위가 높다고 말한다. 수학적으로 순위는 내림차순으로 데이터베이스 문서를 정렬하는 순열 \(\rho_\mathcal{Q}:[1:K]\to[1:K]\)로 지정할 수 있다.
\[\gamma(\mathcal{Q},\mathcal{D}_{\rho_\mathcal{Q}(1)}) \geq \gamma(\mathcal{Q},\mathcal{D}_{\rho_\mathcal{Q}(2)}) \geq \ldots \geq \gamma(\mathcal{Q},\mathcal{D}_{\rho_\mathcal{Q}(K)})\]
- 이 표기법을 사용하여 최상위 순위는 인덱스 값 \(1\)(식별자 \(\rho_\mathcal{Q}(1)\)가 있는 문서에 해당)로 표시되고 가장 낮은 순위는 인덱스값 \(K\)(식별자가 \(\rho_\mathcal{Q}(K)\)인 문서에 해당)로 표시된다.
연관성 함수 (Relevance Function)
다음에서는 정밀도(precision)와 재현율(recall)에 기반한 몇 가지 일반적인 평가 척도의 주요 아이디어를 소개한다.
\(\mathcal{I}:=[1:K]\)가 현재 시나리오에서 데이터베이스 문서의 식별자인 항목(item)의 집합이라고 하자. 평가를 위해 연관(relevant) (또는 양성) 항목의 참조 주석을 사용할 수 있다고 가정한다.
\(\mathcal{I}_\mathcal{Q}:=\mathcal{I}^\mathrm{Ref}_+\subseteq \mathcal{I}\)를 주어진 쿼리 문서 \(\mathcal{Q}\)에 의존하는 연관 항목의 집합이라고 하자. 이 시나리오에서 검색 시스템은 정렬된 문서 목록을 반환한다.
순위 검색 결과를 평가할 수 있는 한 가지 가능성은 순위 매개변수 \(r\in[1:K]\)에 따라 precision 및 recall 값의 전체 계열을 고려하는 것이다.
이후의 편의를 위해 순위가 \(r\)인 문서가 연관성 있을 때 \(1\) 값을 가정하고 그렇지 않으면 \(0\) 값을 가정하는 연관성 함수 \(\chi_\mathcal{Q}:[1:K]\to\{0,1\}\)를 정의한다. 수학적으로 다음과 같이 표현할 수 있다. \[\chi_\mathcal{Q}(r):= \left\{\begin{array}{ll} 1 \quad \mbox{if}\quad \rho_\mathcal{Q}(r) \in \mathcal{I}_\mathcal{Q},\\ 0 \quad \mbox{if}\quad \rho_\mathcal{Q}(r) \in \mathcal{I} \setminus \mathcal{I}_\mathcal{Q}. \end{array}\right.\]
Precision-Recall (PR) 곡선
그런 다음 랭크 \(r\in[1:K]\)의 precision \(\mathrm{P}_\mathcal{Q}(r)\)와 recall \(\mathrm{R}_\mathcal{Q}(r)\)를 다음과 같이 정의한다. \[\mathrm{P}_\mathcal{Q}(r) := \frac{1}{r} \,\,\sum_{k=1}^r \chi_\mathcal{Q}(k), \\ \mathrm{R}_\mathcal{Q}(r) := \frac{1}{|\mathcal{I}_\mathcal{Q}|} \,\,\sum_{k=1}^ r \chi_\mathcal{Q}(k).\]
\(\{(\mathrm{P}_\mathcal{Q}(r),\mathrm{R}_\mathcal{Q}(r)) \mid r\in[1:K] \}\)는 한 축은 precision를 나타내고 다른 축은 recall을 나타내는 2차원 평면에서 시각화된다. 연속된 점들을 결합하면 소위 Precision-recall 곡선 또는 PR 곡선이 생성된다.
간단한 예
- 정의를 설명하기 위해 \(\mathcal{I}:=[1:K]\) 및 \(K=10\) 집합으로 인덱싱된 문서가 있는 예를 고려해보자. 주어진 쿼리 \(\mathcal{Q}\)에 대해 연관 항목 집합이 \(\mathcal{I}_\mathcal{Q}=\{2,7,8,9\}\)라고 가정한다.
- 첫 번째 표에서 \(k\in[1:K]\)에 대한 문서 식별자와 유사성 점수 \(\gamma(\mathcal{Q},\mathcal{D}_k)\in\mathbb{R}\)를 나타낸다. 여기에서 각 문서에 대한 순위 \(\rho_\mathcal{Q}(k)\in[1:K]\)를 도출할 수 있다.
- 두 번째 표에서 문서가 순위에 따라 정렬되어 있으며, 순위, 문서 식별자 및 문서의 연관성을 나타낸다. 이로부터 마지막 두 열에 표시된 대로 \(r\in[1:K]\)에서의 \(\mathrm{P}_\mathcal{Q}(r)\) 값과 \(\mathrm{R}_\mathcal{Q}(r)\) 값을 계산할 수 있다.
- 마지막으로 그림은 결과 PR 곡선을 보여준다.
Image(path_img+"FMP_C7_F21.png", width=600)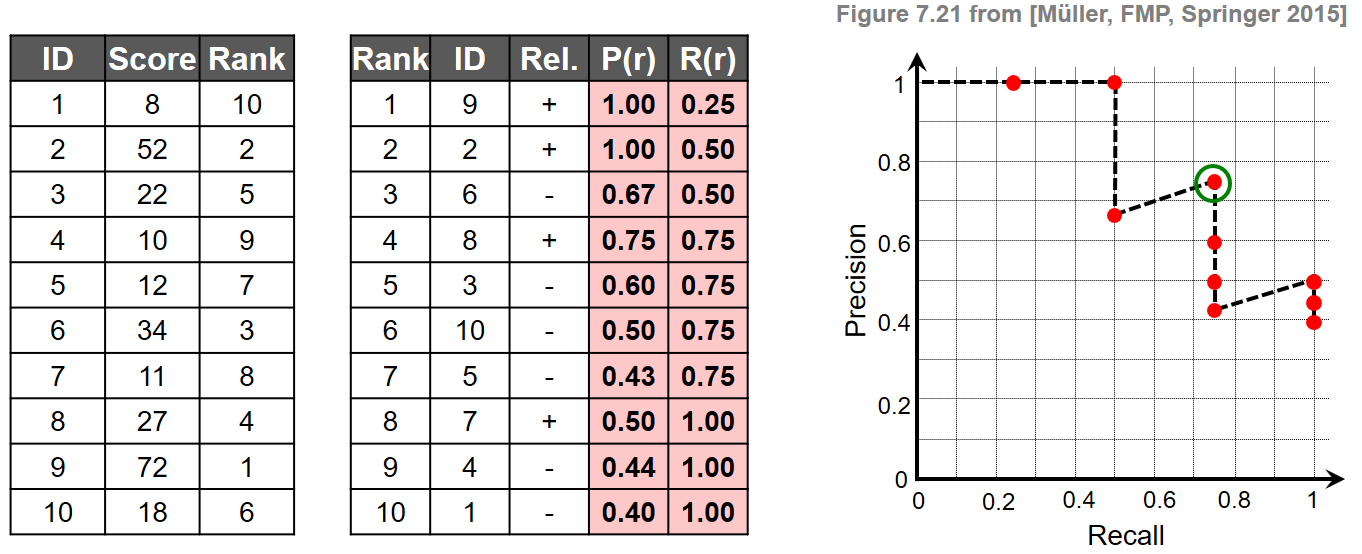
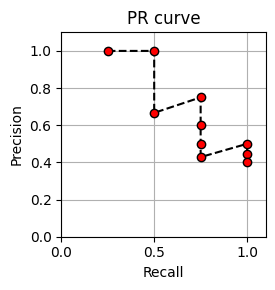
- 이 예에서 연관 항목은 순위 위치 \(r\in\{1,2,4,8\}\)에서 발생한다. 예를 들어 상위 3개 일치 항목에는 \(\mathrm{P}_\mathcal{Q}(3)=2/3\) 및 \(\mathrm{R}_\mathcal{Q}(3)=2/4\)를 산출하는, 4개의 관련 문서 중 2개가 포함되어 있다. 일반적으로 PR 곡선에는 톱니 모양이 있다. \(r^\mathrm{th}\) 문서가 관련이 있으면 정밀도와 재현율이 모두 증가한다. 관련이 없는 경우 재현율은 동일하게 유지되지만 정밀도는 떨어진다. 또한 \(\mathrm{P}_\mathcal{Q}(r)=1\) 값은 모든 상위 \(r\) 일치 항목이 관련됨을 의미한다.
def plot_PR_curve(P_Q, R_Q, figsize=(3, 3)):
fig, ax = plt.subplots(1, 1, figsize=figsize)
plt.plot(R_Q, P_Q, linestyle='--', marker='o', color='k', mfc='r')
plt.xlim([0, 1.1])
plt.ylim([0, 1.1])
ax.set_aspect('equal', 'box')
plt.title('PR curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid()
plt.tight_layout()
return fig, ax# Set up data
I = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
score = np.array([8, 52, 22, 10, 12, 34, 11, 27, 72, 18])
I_Q = np.array([2, 7, 8, 9])
# Compute rank and sort documents according to rank
K = len(I)
index_sorted = np.flip(np.argsort(score))
I_sorted = I[index_sorted]
rank = np.argsort(index_sorted) + 1
rank_sorted = np.arange(1, K+1)
# Compute relevance function X_Q (indexing starts with zero)
X_Q = np.zeros(K, dtype=bool)
for i in range(K):
if I_sorted[i] in I_Q:
X_Q[i] = True
# Compute precision and recall values (indexing starts with zero)
M = len(I_Q)
P_Q = np.zeros(K)
R_Q = np.zeros(K)
for i in range(K):
r = rank_sorted[i]
P_Q[i] = np.sum(X_Q[:r]) / r
R_Q[i] = np.sum(X_Q[:r]) / M
# Arrange output as tables
df1 = pd.DataFrame({'ID': I, 'Score': score, 'Rank': rank})
df2 = pd.DataFrame({'Rank': rank_sorted, 'ID': I_sorted,
'$\chi_\mathcal{Q}$': X_Q,
'P(r)': P_Q,
'R(r)': R_Q})
fig, ax = plot_PR_curve(P_Q, R_Q)
# Visualize tables and figure in floating box
ipd.display(df1)
ipd.display(df2)| ID | Score | Rank | |
|---|---|---|---|
| 0 | 1 | 8 | 10 |
| 1 | 2 | 52 | 2 |
| 2 | 3 | 22 | 5 |
| 3 | 4 | 10 | 9 |
| 4 | 5 | 12 | 7 |
| 5 | 6 | 34 | 3 |
| 6 | 7 | 11 | 8 |
| 7 | 8 | 27 | 4 |
| 8 | 9 | 72 | 1 |
| 9 | 10 | 18 | 6 |
| Rank | ID | $\chi_\mathcal{Q}$ | P(r) | R(r) | |
|---|---|---|---|---|---|
| 0 | 1 | 9 | True | 1.000000 | 0.25 |
| 1 | 2 | 2 | True | 1.000000 | 0.50 |
| 2 | 3 | 6 | False | 0.666667 | 0.50 |
| 3 | 4 | 8 | True | 0.750000 | 0.75 |
| 4 | 5 | 3 | False | 0.600000 | 0.75 |
| 5 | 6 | 10 | False | 0.500000 | 0.75 |
| 6 | 7 | 5 | False | 0.428571 | 0.75 |
| 7 | 8 | 7 | True | 0.500000 | 1.00 |
| 8 | 9 | 4 | False | 0.444444 | 1.00 |
| 9 | 10 | 1 | False | 0.400000 | 1.00 |
PR Curve의 break-even point
특정 쿼리의 경우 PR 곡선은 순위 검색 결과의 전반적인 품질에 대해 좋은 인상을 준다. 그러나 전체 정밀도 및 재현율 값을 처리하는 것은 상당히 번거로울 수 있다. 따라서 이 PR 값 계열을 전체 검색 성능에 대한 몇 가지 특성 정보를 포함하는 단일 평가 측정으로 줄이는 경우가 많다. 그러한 척도 중 하나는 PR 곡선의 break-even point로, 정밀도가 재현율과 동일할 때의 양의 값으로 정의된다.
위 예시에서 break-even point은 \(\mathrm{P}_\mathcal{Q}(4)=\mathrm{R}_\mathcal{Q}(4)=0.75\)이다. 순위 목록의 상위 \(|\mathcal{I}_\mathcal{Q}|\) 항목 중 관련 문서가 하나 이상 있는 경우에만 break-even point가 존재한다.
또한 이 경우 break-even point은 순위 \(r=|\mathcal{I}_\mathcal{Q}|\)의 정밀도(또는 재현율)에 해당한다. \[\mathrm{P}_\mathcal{Q}(|\mathcal{I}_\mathcal{Q}|) = \mathrm{R}_\mathcal{Q}(|\mathcal{I}_\mathcal {Q}|)\]
또 다른 척도로 PR곡선의 정밀도와 재현율에 해당하는 F-측정값(F-measure)을 고려할 수 있다. \[\mathrm{F}_\mathcal{Q}(r) = 2\cdot \frac{\mathrm{P}_\mathcal{Q}(r)\cdot \mathrm{R}_\mathcal{Q}(r)}{\mathrm{P}_\mathcal{Q}( r) + \mathrm{R}_\mathcal{Q}(r)}\] 를 \(\mathrm{P}_\mathcal{Q}(r)\) 및 \(\mathrm{R}_\mathcal{Q}(r)\)의 F-측정값이라고 하자.
- \(\mathrm{P}_\mathcal{Q}(r)=0\) 및 \(\mathrm{R}_\mathcal{Q}(r)=0\)인 경우 \(\mathrm{F }_\mathcal{Q}(r)=0\)이다.
그런 다음 PR 곡선의 최대 F-측정값은 다음과 같이 정의된다. \[\mathrm{F}_\mathcal{Q}^\mathrm{max} := \max_{r\in[1:K]} \mathrm{F}_\mathcal{Q}(r)\]
위의 예에서 최대 F-측정값은 \(\mathrm{F}_\mathcal{Q}^\mathrm{max}=0.75\)이며 break-even point와 같다. 그러나 일반적으로 두 측정값이 일치할 필요는 없다.
# Break-even point
BEP = P_Q[M-1]
# Maximal F-measure
sum_PR = P_Q + R_Q
sum_PR[sum_PR==0] = 1 # Avoid division by zero
F_Q = 2 * (P_Q * R_Q) / sum_PR
F_max = F_Q.max()
# Figure
fig, ax = plot_PR_curve(P_Q, R_Q, figsize=(4, 4))
ax.plot(BEP, BEP, color='green', marker='o', fillstyle='none', markersize=15)
ax.set_title('PR curve with break-even point (green circle)')
plt.show()
print('Break-even point = %.2f' % BEP)
print('F_Q = ', np.round(F_Q, 2))
print('F_max = %.2f' % F_max)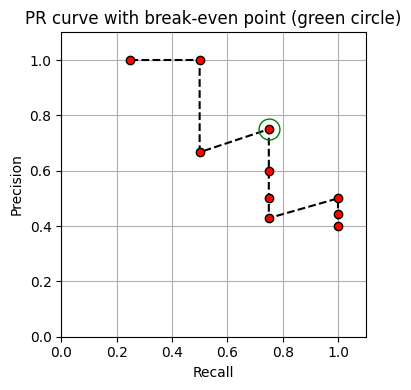
Break-even point = 0.75
F_Q = [0.4 0.67 0.57 0.75 0.67 0.6 0.55 0.67 0.62 0.57]
F_max = 0.75Average Precision
이제 특정 순위 위치에서 정밀도 값을 보고 그 결과를 평균화하는 평가 척도를 고려한다. 평균 정밀도(average precision) \(\overline{\mathrm{P}}_\mathcal{Q}\)는 다음과 같이 정의된다. \[\overline{\mathrm{P}}_\mathcal{Q}:= \frac{1}{|\mathcal{I}_\mathcal{Q}|} \sum_{r=1}^K \mathrm{P }_\mathcal{Q}(r)\chi_\mathcal{Q}(r)\]
이 정의에서 정밀도 \(\mathrm{P}_\mathcal{Q}(r)\)는 \(\chi_\mathcal{Q}(r)=1\)인 경우에만 고려된다. 즉, 재현율 수준이 변경되는 순위에서만 평균이 계산된다. 예를 들어, 위의 검색 결과의 경우 평균 정밀도는 다음과 같다. \[\overline{\mathrm{P}}_\mathcal{Q} = \frac{1}{4} (1 + 1 + 0.75 + 0.5) = 0.8125.\]
break-even point와 최대 F-measure의 경우, 평균 정밀도는 0과 1 사이이며 모든 관련 문서가 최상위에 있는 경우에만 값 1을 가정한다. 평균 정밀도의 한 가지 장점은 다른 두 가지 척도와 달리 전체 순위 목록을 고려한다는 것이다. 예를 들어, 위의 예에서 \(\chi_\mathcal{Q}(8)\) 및 \(\chi_\mathcal{Q}(9)\) 값을 교환하면(따라서 관련 문서의 순위가 한 단계 낮아짐) break-even point와 최대 F-측정은 변경되지 않은 반면, 평균 정밀도는 \(\bar{\mathrm{P}}_\mathcal{Q} = (1 + 1 + 0.75 + 0.44)/4 = 0.7975\)로 감소한다.
P_average = np.sum(P_Q * X_Q) / len(I_Q)
print('Average precision =', P_average)Average precision = 0.8125Mean Average Precision
지금까지 단일 쿼리 문서 \(\mathcal{Q}\)에 대한 평가 방법을 살펴보았다. 실제로 검색 시스템의 성능을 평가할 때 주어진 애플리케이션 시나리오 내에서 사용자가 필요로 하는 일반적인 정보를 반영하는 다양한 쿼리를 사용해야 한다. 단일 평가의 숫자를 얻기 위해 이러한 모든 값에 대한 평균을 취하여 쿼리 종속 값을 결합하는 경우가 많다.
예를 들어 평균 정밀도의 경우를 살펴보자. \(\{\mathcal{Q}_1,\ldots,\mathcal{Q}_J\}\)를 평가에서 고려할 쿼리 문서 집합이라고 하자. 그런 다음 각 \(j\in[1:J]\)에 대해 \(\overline{\mathrm{P}}_{\mathcal{Q}_j}\) 값을 얻는다.
Mean average precision 또는 MAP은 다음과 같이 정의된다. \[\overline{\mathrm{P}} := \frac{1}{J} \sum_{j=1}^J \overline{\mathrm{P}}_{\mathcal{Q}_j}\]
구현
def compute_prf_metrics(I, score, I_Q):
"""Compute precision, recall, F-measures and other
evaluation metrics for document-level retrieval
Args:
I (np.ndarray): Array of items
score (np.ndarray): Array containing the score values of the times
I_Q (np.ndarray): Array of relevant (positive) items
Returns:
P_Q (float): Precision
R_Q (float): Recall
F_Q (float): F-measures sorted by rank
BEP (float): Break-even point
F_max (float): Maximal F-measure
P_average (float): Mean average
X_Q (np.ndarray): Relevance function
rank (np.ndarray): Array of rank values
I_sorted (np.ndarray): Array of items sorted by rank
rank_sorted (np.ndarray): Array of rank values sorted by rank
"""
# Compute rank and sort documents according to rank
K = len(I)
index_sorted = np.flip(np.argsort(score))
I_sorted = I[index_sorted]
rank = np.argsort(index_sorted) + 1
rank_sorted = np.arange(1, K+1)
# Compute relevance function X_Q (indexing starts with zero)
X_Q = np.isin(I_sorted, I_Q)
# Compute precision and recall values (indexing starts with zero)
M = len(I_Q)
P_Q = np.cumsum(X_Q) / np.arange(1, K+1)
R_Q = np.cumsum(X_Q) / M
# Break-even point
BEP = P_Q[M-1]
# Maximal F-measure
sum_PR = P_Q + R_Q
sum_PR[sum_PR == 0] = 1 # Avoid division by zero
F_Q = 2 * (P_Q * R_Q) / sum_PR
F_max = F_Q.max()
# Average precision
P_average = np.sum(P_Q * X_Q) / len(I_Q)
return P_Q, R_Q, F_Q, BEP, F_max, P_average, X_Q, rank, I_sorted, rank_sorted# excercise 7.14
I = np.array([1, 2, 3, 4, 5, 6, 7, 8])
score = np.array([0.7, 2.6, 3.6, 3.5, 3.2, 3.7, 1.5, 3.1])
I_Q = np.array([2, 3, 4, 8])
output = compute_prf_metrics(I, score, I_Q)
P_Q, R_Q, F_Q, BEP, F_max, P_average, X_Q, rank, I_sorted, rank_sorted = output
# Arrange output as tables
score_sorted = np.flip(np.sort(score))
df = pd.DataFrame({'Rank': rank_sorted, 'ID': I_sorted,
'Score': score_sorted,
'$\chi_\mathcal{Q}$': X_Q,
'P(r)': P_Q,
'R(r)': R_Q,
'F(r)': F_Q})
fig, ax = plot_PR_curve(P_Q, R_Q, figsize=(3,3))
ax.plot(BEP, BEP, color='green', marker='o', fillstyle='none', markersize=15)
ax.set_title('PR curve')
# Visualize tables and figure in floating box
ipd.display(df)
print('Break-even point = %.2f' % BEP)
print('F_max = %.2f' % F_max)
print('Average precision =', np.round(P_average, 5))| Rank | ID | Score | $\chi_\mathcal{Q}$ | P(r) | R(r) | F(r) | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 6 | 3.7 | False | 0.000000 | 0.00 | 0.000000 |
| 1 | 2 | 3 | 3.6 | True | 0.500000 | 0.25 | 0.333333 |
| 2 | 3 | 4 | 3.5 | True | 0.666667 | 0.50 | 0.571429 |
| 3 | 4 | 5 | 3.2 | False | 0.500000 | 0.50 | 0.500000 |
| 4 | 5 | 8 | 3.1 | True | 0.600000 | 0.75 | 0.666667 |
| 5 | 6 | 2 | 2.6 | True | 0.666667 | 1.00 | 0.800000 |
| 6 | 7 | 7 | 1.5 | False | 0.571429 | 1.00 | 0.727273 |
| 7 | 8 | 1 | 0.7 | False | 0.500000 | 1.00 | 0.666667 |
Break-even point = 0.50
F_max = 0.80
Average precision = 0.60833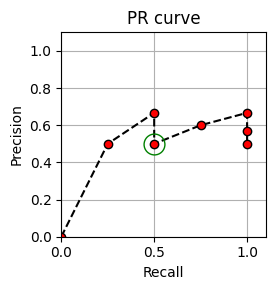
출처:
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C7/C7S3_CommonSubsequence.html
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C7/C7S3_VersionIdentification.html
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C7/C7S3_Evaluation.html
\(\leftarrow\) 8.3. 오디오 매칭